Vektor bukan bilangan biasa, sehingga
perkalian biasa tidak bisa langsung digunakan pada vektor. Kita harus
menggunakan perkalian vektor. Perkalian vektor terdiri dari dua jenis, yaitu
perkalian titik dan perkalian silang. Pada kesempatan kali ini, materi yang
akan dibahas adalah mengenai perkalian silang. Apa itu perkalian silang?
Perkalian silang merupakan perkalian yang menghasilkan besaran vektor atau
dikenal dengan “Cross Product”.
Sifat-sifat perkalian silang vektor adalah sebagai berikut :
Dari ke-5 sifat perkalian silang tersebut, mari kita uji beberapa sifat perkalian silang apakah sifat tersebut adalah benar atau sebaliknya. Sebelum melakukan pengujian, kita misalkan A =
A1i + A2j +A3k, kemudian B =
B1i + B2j +B3k, dan C
= C1i + C2j +C3k. Pengujian yang pertama adalah mengambil sifat ke-4 :
Dari hasil tersebut, dapat disimpulkan bahwa pembuktian dari sifat ke-4 adalah benar adanya. Setelah itu, mari kita lakukan pengujian sekali lagi, untuk membuktikan bahwa sifat perkalian tersebut adalah benar. Mari kita lakukan pada pengujian yang kedua dengan mengambil sifat perkalian silang yang ke-3 :
2. Metode biasa : Untuk melakukan metode biasa ini, langkah awal yang harus dilakukan tidak berbeda dengan langkah awal (langkah a) dengan menggunakan metode Sarrus. Perbedaannya adalah, setelah melakukan langkah awal, langkah berikutnya adalah :
Dari hasil tersebut, dapat disimpulkan bahwa pembuktian dari sifat ke-4 adalah benar adanya. Setelah itu, mari kita lakukan pengujian sekali lagi, untuk membuktikan bahwa sifat perkalian tersebut adalah benar. Mari kita lakukan pada pengujian yang kedua dengan mengambil sifat perkalian silang yang ke-3 :
Pada sifat yang ke-3 ini, juga terbukti bahwa perkalian dengan vektor yang nilainya sama, akan menghasilkan nilai 0. Pada perkalian ini, metode atau cara penyelesaian yang digunakan adalah menggunakan beberapa cara, yaitu:
1. Menggunakan cara Sarrus
2. Menggunakan cara biasa.
Pada dasarnya, kedua metode tersebut dapat melakukan penyelesaian untuk menghadapi persoalan dari vektor perkalian silang. Dan kedua cara tersebut tidak terlalu sulit untuk dipahami. Lebih jelasnya, simak penjelasan tentang kedua cara penyelesaian tersebut dengan seksama!
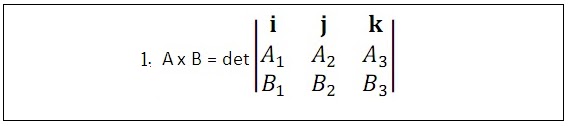
1. Metode Sarrus : metode ini
digunakan untuk mencari determinan matriks yang berdimensi 3x3. Tetapi, cara Sarrus ini dapat
digunakan untuk menghitung perkalian silang pada vektor. Sebagai contoh : A =[ A1 A2 A3 ]
dan B =[ B1 B2 B3 ]. Untuk menggunakan cara Sarrus, langkah pertama yang harus dilakukan adalah :
a) Tulis vektor A dan vektor B ke dalam langkah seperti di atas. Dengan menggunakan baris pertama dengan variable i, j, dan k. Sedangkan yang baris kedua adalah nilai dari vektor A dan baris ketiga adalah nilai dari vektor B.
b) Setelah itu, tulis kembali dari kolom i, dan kolom j di sebelah kanan dari kolom k. Untuk penulisannya, pada kolom i = [ i A1 B1 ] sedangkan kolom j adalah = [ j A2 B2].
c) Kemudian langkah yang terakhir adalah menghitung nilai dari langkah 2 dengan cara seperti berikut ini :
Pada langkah di atas, untuk melakukan perhitungan samah halnya untuk mencari determinan. Sehingga, akan mendapatkan hasil sama halnya dengan metode Sarrus.
Contoh Soal!
1. Diketahui terdapat vektor A bernilai A = [1,2,3] dan vektor B bernilai B = [4,5,6]. Kerjakan dengan metode biasa atau metode Sarrus?
Jawab:
Menggunakan metode Sarrus, maka :
A x B = 12i + 12j + 5k - 8k - 15i - 6j = -3i + 6j - 3k
A x B = [-3 6 -3]
Sumber :